cours
1. Chapitre I: Représentation des nombres
Contexte Historique:
Il y a 4000ans, les Babyloniens inventèrent la base de 60 pour 12 falanges et 5 doigts et la numérotation de position. Les romains n'utilisaient pas la numérotation de position.
Au 4ème siècle en Inde on utilise le zéro, la numérotation de position et la base de 10. Les calcules deviennent possible.
Au 17ème siècle la prmière machine à calculer en base de 2 est inventée par l'Allemand Leibneitz.
Les premier ordinateurs stokaient leurs données sur des cartes perforées et l'unité d'information est le bit. Dans un octet il y a 8 bits.
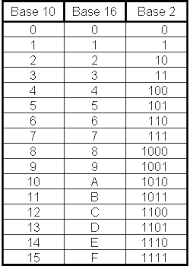
Tableau des base de 10 de 2 et de 16:
Les Convertions:
1. De la base de 10 à la base de 2 et de la base de 10 à la base de 16
Pour passer de la base de 10 à la base de 2 il suffit de diviser le nombre en base de 10 par 2 et de continuer jusqu'à ce que le quotient valle 0 et on lit le résultat (le reste de chaque division) de droite à gauche.
Pour passer de la base de 10 à la base de 16 il suffit de diviser le nombre en base de 10 par 16 et de continuer jusqu'à ce que le quotient valle 0 et on lit le résultat (le reste de chaque division) de droite à gauche.
2. De la base de 2 à la base de 10 et de la base de 16 à la base de 10
Pour passer d'un nombre en base de 2 en base de 10 il suffit de multiplié le nombre en base de 2 par 2 puissance le rang de la valeur multipliée.
Par exemple 101 (2) = 1 x 2^2 + 0 x 2^1 + 1 x 2^0
=5 (10)
Pour passer d'un nombre en base de 16 en base de 10 il suffit de multiplié le nombre en base de 16 par 16 puissance le rang de la valeur multipliée.
Par exemple 3F (16) = 3 x 16^1 + 15 x 16^0
=63 (10)
3. De la base de 2 à la base de 16 et de la base de 16 à la base de 2
Pour passer de la base de 2 à la base de 16 il suffit de prendre 4 valeurs de la base de 2 et de trouver leur correspondant en base de 16. Pour passer de la base de 16 à la base de 2 il suffit de prendre 1 valeurs de la base de 16 et de trouver son correspondant en base de 2.
4. Les nombres négatifs sur 8 bits et les nombresà virgules flotante
Pour représenter un entier négatif -m sur n bit(s):
- on écrit l'entier positif m sur n bit(s) (rajouter éventuellement des 0 à gauche).
- on remplace chaque 0 par un 1 et chaque 1 par 0
- on rajoute 1
Pour représenter un nombre à virgule flotante on multiplie la partie décimal par 2 et on garde la partieentière dans certain cas la conversion ne s'arrête jamais.

Chapitre II Encodage des charactère et exprésion booléens.
Introduction:
Boole en 1856 a possé les bases d'une algèbre binaire n'utilisant que des 1 ou des 0 (ou des vrai ou des faux). L'algèbre de Boole permet de comprendre le fonctionnement des mémoires et micro processeur.
Les charactères doivent être codé exactement chacun avec une représentation différentes.
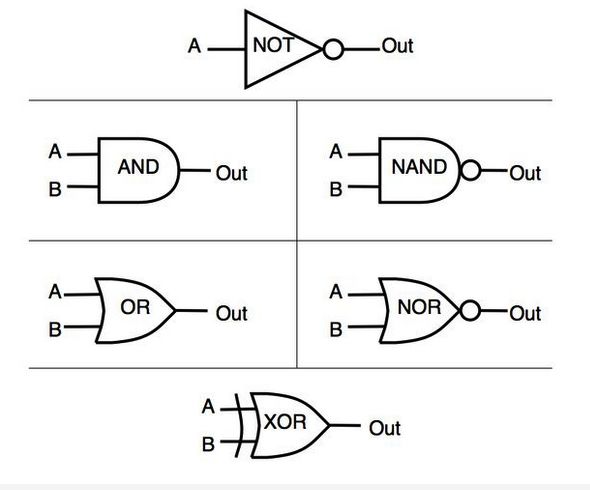
Les portes logiques
Voici les schémas des représentation des tables de vérité sous la forme de porte logique. Nous pouvons voir tout en haut la porte logique du "non" (not en anglais) qui est la négation qui ne donne des 1 que lorsque A vaut 0. Puis sur la deuxième ligne en haut à droite il y a la porte logique de la conjonction donc le "et" (en anglais and) qui ne donne des 1 que lorsque A et B valent 1 en même temps. De plus, toujours sur la deuxième ligne mais à gauche il y a la porte logique de la conjonction mais en négatif "non et"(nand) c'est à dire qu'il y aura un 1 lorsque A et B vaudront 1 ou 0 mais pas 1 en même temps. Outre cela, nous pouvons voir tout en bas la porte logique du "xor" qui est le ou exclusif c'est à dire qui ne donne des 1 que lorsqu'il y a A ou B mais pas les deux en même temps. Puis sur la troisième ligne en bas à droite il y a la porte logique de la disjonction donc le "ou" (en anglais or) qui ne donne des 1 lorsqu'il y a A ou B ou les deux en même temps. De plus, toujours sur la troisième ligne mais à gauche il y a la porte logique de la disjonction mais en négatif "non ou"(nor) c'est à dire qu'il y aura un 1 lorsqu'il y aura A ou B, et un 1 lorsque A et B vaudrons 0 tout les deux .
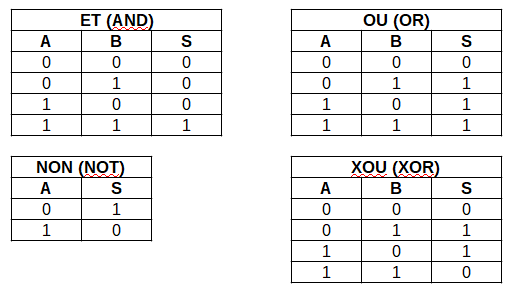
Les tables de vérités
Voici les schémas des représentation des tables de vérité. Nous pouvons voir en haut à droite il y a la table de vérité de la conjonction donc le "et" (en anglais and) qui ne donne des 1 que lorsque A et B valent 1 en même temps. Nous pouvons voir également à droit mais en bas la table de vérité du "non" (not en anglais) qui est la négation qui ne donne des 1 que lorsque A vaut 0. Outre cela, nous pouvons voir tout en bas à gauche la table de vérité du "xor" qui est le ou exclusif c'est à dire qui ne donne des 1 que lorsqu'il y a A ou B mais pas les deux en même temps. Puis sur en haut à gauche il y a la porte logique de la disjonction donc le "ou" (en anglais or) qui ne donne des 1 lorsqu'il y a A ou B ou les deux en même temps.
Chapitre III: Les types construis
Dans la console:
I Tuples:
Dans la console:
II Listes:
Dans la console:
>>> dico={'Axel':20,'Szymanska':2,'Damien':-4000}
>>> dico.keys()
dict_keys(['Axel', 'Szymanska', 'Damien'])
>>> dico.values()
dict_values([20, 2, -4000])
>>> dico.items()
dict_items([('Axel', 20), ('Szymanska', 2), ('Damien', -4000)])
>>> dico
{'Axel': 20, 'Damien': -4000, 'Szymanska': 2}
>>> dico['Gabriel']=3.2
>>> dico
{'Axel': 20, 'Damien': -4000, 'Gabriel': 3.2, 'Szymanska': 2}
>>> dico['Gabriel']=16
>>> dico
{'Axel': 20, 'Damien': -4000, 'Gabriel': 16, 'Szymanska': 2}
>>> dico.pop('Gabriel')
16
>>> dico
{'Axel': 20, 'Damien': -4000, 'Szymanska': 2}
>>> len(dico)
3
III Dictionnaires:
Un dictionnaire associe des clés à des valeurs, ici Axel avec 20 etc... un dictionnaire s'écrit avec des accolade.
Dico.key renvoie dans la console seulement les clefs.
Dico.values renvoie dans la console seulement les valeurs.
dico.items renvoie tout les item dans la console.
dico renvoie toutes les clefs associées avec leurs valeurs entre accolade.
On peut ajouter des clefs avec leurs valeurs dans un dictionnaire (il sera placé n'importe où entre les accolades)
On peut changer la valeur d'une clef.
dico.pop retire la dernière clef et la dernière valeur contenues dans les accolades.
len(dico) affiche le nombre de paire que contiens le dictionnaire.
Chapitre IV: Les Tris
Tri à bulle, tri fusion, tri sélection, tri insertion...